Guía práctica para comprender tablas de datos no agrupados
Cuando analizamos una muestra sin segmentar, medir la variabilidad se vuelve fundamental para captar la verdadera esencia del comportamiento de los valores. La dispersión revela qué tan alejados están los puntos respecto al promedio, y eso impacta directamente en la precisión del análisis estadístico.
Es recomendable calcular la desviación estándar o el rango intercuartílico para obtener una imagen clara de la fluctuación que presentan los elementos. Ignorar esta fase puede llevar a conclusiones erróneas sobre la estabilidad o la homogeneidad del conjunto observado.
El seguimiento de la variabilidad contribuye a entender la consistencia de la información y ayuda a detectar posibles anomalías o tendencias ocultas dentro de cada muestra. Al interpretar cada número individual sin agrupar, se obtiene una perspectiva más detallada y auténtica del fenómeno estudiado.
Cómo identificar y leer cada elemento en una tabla de datos no agrupados
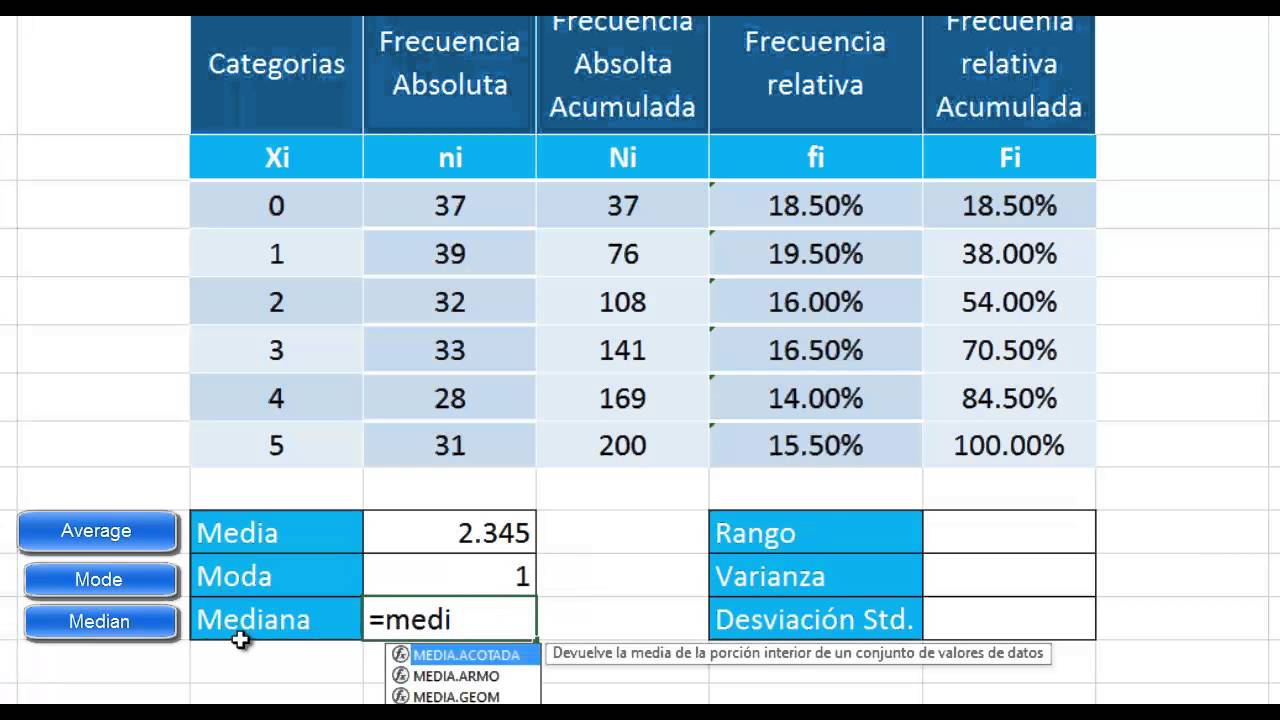
Observa primero las valores individuales que componen la muestra; cada uno representa una observación única sin clasificar en categorías. A su lado, la frecuencia indica cuántas veces se repite cada valor en el conjunto. Reconocer estos pares es fundamental para medir la variabilidad del fenómeno en cuestión.
La dispersión se refleja en la diferencia entre los valores más altos y bajos registrados. Si estas diferencias son amplias, la volatilidad en la información aumentará. Por ello, identificar correctamente elementos como la media o mediana puede ayudar a resumir el comportamiento central de la muestra.
Frecuencia y su función en la interpretación
No ignores la frecuencia: es la clave para calcular estadísticas descriptivas como la moda, que señala el valor más habitual. Entender cuántas veces ocurre cada dato permite intuir la relación entre la dispersión y la concentración de valores, dando pistas sobre la homogeneidad o heterogeneidad del conjunto.
Relación entre muestra, variabilidad y estadística
Una muestra con poca variabilidad exhibe menor dispersión y, por tanto, resultados más consistentes. La estadística aplicada a estos números convierte esa información en conclusiones reales, facilitando la anticipación y comparación de patrones. Reconocer y leer cada elemento correctamente es la puerta de entrada para explotar al máximo el potencial de la información recogida.
Métodos para calcular medidas de tendencia central en datos no agrupados
Promedio aritmético es el método más directo y común. Simplemente sumas todos los valores presentes en la muestra y divides entre el número total de observaciones. Este valor refleja el centro exacto de tus puntos, aunque puede verse afectado por valores extremos, lo que influye en la variabilidad y dispersión de la distribución.
Mediana resulta útil cuando la muestra contiene valores atípicos o la distribución no es simétrica. Ordena todos los números y selecciona el valor que queda justo en el medio. Si la cantidad de datos es par, considera el promedio de los dos centrales. Así, esta medida minimiza el efecto de la dispersión irregular y ofrece un punto de referencia sólido dentro del análisis estadístico.
Moda identifica el valor que aparece con mayor frecuencia en el conjunto. Es particularmente relevante cuando el interés reside en detectar tendencias repetidas o patrones predominantes en la colección de datos. En muestras con múltiples modas, se puede hablar de distribuciones bimodales o multimodales, lo que afecta directamente el enfoque para explorar la variabilidad interna.
Para obtener una visión completa, conviene complementar estas medidas con índices de dispersión, como la desviación estándar, que contextualizan mejor la concentración y dispersión alrededor de la tendencia central.
Procedimientos para determinar la variabilidad y dispersión en tablas simples
Calcula la frecuencia de cada valor para establecer la distribución dentro de la muestra. La variabilidad surge al identificar cuántos datos se alejan de la media aritmética o la mediana. Un análisis preciso inicia con el cálculo de la media muestral y la identificación del valor central.
Métodos clave para medir la dispersión
- Rango: Diferencia entre el valor máximo y mínimo. Indica la amplitud total de la muestra, pero puede ser sensible a valores extremos.
- Varianza: Promedio de las desviaciones al cuadrado respecto a la media. Refleja la dispersión efectiva y permite comparaciones estadísticas.
- Desviación típica: Raíz cuadrada de la varianza, proporciona un indicador intuitivo sobre cómo se distribuyen los datos respecto a la media.
- Coeficiente de variación: Relación entre la desviación típica y la media, ideal para comparar dispersión entre muestras con escalas distintas.
Pasos prácticos
- Recopila los valores y asocia cada uno con su frecuencia correspondiente.
- Calcula la media ponderada con frecuencias para reflejar la tendencia central.
- Obtén la diferencia de cada dato respecto a la media y eleva al cuadrado.
- Multiplica cada resultado por la frecuencia y suma todos esos valores.
- Divide la suma total por el número total de observaciones menos uno (varianza muestral).
- Extrae la raíz cuadrada para obtener la desviación estándar.
Este procedimiento cuantifica cuánto se dispersan los valores, facilitando el análisis de la estructura interna de la información y ayudando a identificar heterogeneidades dentro del conjunto. Sin estas medidas, interpretar tendencias o detectar anomalías sería difícil.
Interpretación paso a paso de frecuencias absolutas y relativas
Identifica primero la frecuencia absoluta: es el conteo real de ocurrencias de cada valor dentro de la muestra. Por ejemplo, si un valor aparece 15 veces, su frecuencia absoluta es 15. Esto te permite valorar la cantidad exacta y comparar la presencia de diferentes elementos en el conjunto.
Calcula la frecuencia relativa: divide cada frecuencia absoluta por el total de observaciones en la muestra. Este cociente representa la proporción o porcentaje que ese valor representa respecto al total, facilitando la comparación cuando los tamaños de muestras varían.
Análisis de variabilidad y dispersión
La variabilidad se refleja en cómo las frecuencias se distribuyen entre los valores. Si una frecuencia absoluta concentra gran parte del total, la dispersión es baja y el conjunto es homogéneo; si las frecuencias están distribuidas de forma más pareja, la dispersión aumenta, indicando diversidad en la muestra.
Observar ambas frecuencias en conjunto ayuda a visualizar patrones: la frecuencia absoluta muestra la cantidad directa y la relativa revela su peso proporcional. Por ejemplo, una frecuencia alta pero relativa baja indica un valor común en una muestra grande, mientras que una alta relativa con baja frecuencia absoluta puede señalar un efecto en una muestra pequeña.
Recomendaciones para interpretar
Evita confiar solo en frecuencias absolutas. Sin conocer el tamaño total, el análisis puede ser engañoso. Siempre complementa con frecuencias relativas para entender la relevancia real de cada valor.
Busca consistencia en la dispersión: valores con frecuencias similares sugieren poca variabilidad, mientras que valores extremos en la frecuencia absoluta o relativa indican que la estadística de dispersión debe considerarse con precisión, usando medidas como rango o desviación estándar.
Errores comunes al analizar tablas de datos sin agrupar y cómo evitarlos
No ignores la dispersión de la muestra. Muchos se enfocan solo en la frecuencia de ciertos valores y olvidan que la variabilidad es igual de determinante para un buen análisis estadístico. Examina siempre la amplitud de los puntos tenidos en cuenta y calcula medidas como desviación estándar o rango intercuartílico. Esto evita conclusiones sesgadas basadas en un solo valor central.
No confíes únicamente en promedios. Un promedio puede ocultar picos o patrones relevantes. Por ejemplo, una media alta junto con alta dispersión puede indicar datos muy dispersos y sin tendencia clara. Complementa con la mediana y moda para obtener una visión más completa.
No omitas revisar la consistencia de las frecuencias. Asegúrate de que la suma de frecuencias coincida con el tamaño de la muestra y que no haya valores extemporáneos o erróneos. Errores en estos conteos alteran todo el análisis y llevan a interpretaciones incorrectas.
No subestimes el valor del orden. Analizar el conjunto en desorden puede dificultar detectar patrones o valores atípicos. Ordenar las observaciones facilita identificar tendencias y calcular percentiles o cuartiles con precisión.
No mezcles datos heterogéneos sin segmentar. Combinar diferentes tipos de información sin discriminar variables clave confunde el análisis y genera conclusiones poco claras. Divide la muestra según características relevantes antes de profundizar en la estadística descriptiva.



